Diskontlaşdırma
2019-08-22 | Maliyyə menecmenti |Maliyyə sahəsində bir çox hallarda (investisiyaların qoyulması, səhmlərin alınması, yeni layihələrin qiymətləndirilməsi və s. hallarda) məbləğlərin diskontlaşdırılmasından istifadə edilir. Bundan başqa, məbləğlərin diskontlaşdırılmasını bir çox maliyyə hesabatlarının beynəlxalq standartları tələb edir:
- Müştərilərlə müqavilələr üzrə gəlirlər. IFRS 15;
- "İcarələr. İFRS 16";
- Aktivlərin Qiymətdən düşməsi. IAS 36;
- Yaradılmış ehtiyat fondları, Şərti öhdəliklər və Şərti aktivlər. IAS 37;
- Maliyyə alətləri: Tanınma və ölçülmə. IAS 39 və s.
Misal üçün, "İcarələr. İFRS 16" standartında icarə müddətinin başlanması tarixində icarəçi icarə öhdəliyini həmin tarixdə ödənilməmiş icarə ödənişlərinin diskontlaşdırılmış dəyərilə ölçməlidir.
Bəs məbləğin diskontlaşdırılması nədir? Nə cür hesablanır?
Diskontlaşdırmanın mahiyyətini izah etmək üçün gəlin bu əməliyyatın izahını sondan başlayaq.
Müəssisə bankda depozit hesab açmışdır və hesaba 2 illik müddətinə 1 000 manat əmanət qoymuşdur. Əmanət üzrə illik faiz dərəcəsi 10%-dir. Bir ildən sonra bu məbləğ 1 100 manat olacaqdır: əsas məbləğ 1 000 manat + faiz əlavəsi 100 manat (1 000*10%). Bir ildən sonra siz hesabdan 1 100 manat çıxara bilərsiniz.
Riyazi olaraq düstur bu cür olacaqdır
1 000 * (1+10%) və ya 1 000 * (1.10) = 1 100
İki ildən sonra 1 000 manat olacaqdır 1 210 manat (1 000 manat + birinci ilin faizi 100 manat + ikinci ilin faizi 110 = 1 100*10%). İki il üzrə bankda olan əmanət hesabının artım düsturu olacaqdır: (1 000*1.10)*1.10 = 1 210.
İllər keçdikcə əmanətin məbləği artacaqdır. Bankdan alacağınız məbləğin faizini bir, iki, üç və s. ilərdən sonra müəyyən etmək üçün əmanət məbləğini əmsala vurmaq lazımdır:
(1+R)n
Burada:
- R - faiz dərəcəsi (10% və ya 0.10);
- n - illər.
Bizim misalda olacaqdır: 1 000 * (1 + 0.10)2 = 1 210.
Misaldan göründüyü kimi iki ildən sonra bank depozitində olan pulun məbləği illik bank faizinin dərəcəsindən asılıdır. Əmanətlər üzrə illik bank faizi çox olduqca məbləğ də artacaqdır. Əmanətlər üzrə bankın illik faiz dərəcəsi 12% olsa idi, iki ildən sonra müəssisə bankdan 1 254.40 manat götürə biləcəkdi: 1 000 * (1+0.12)2 = 1 254.40.
Beləliklə, bu üsul ilə depozitə qoyulan məbləğin istənilən ildən sonra məbləğini hesablamaq mümkündür. Pulun gələcəkdə dəyərinin hesablanmasına inqilis dilində "compoundinq" deyilir. Azərbaycan dilində bu termin "mürəkkəb faizin hesablanması" kimi tərcümə edilir. Bu termini "faizlərin toplanması" kimi də tərcümə etmək olar.
Aydındır ki, banka qoyulmuş əmanətlər illər keçdikcə illik faiz dərəcəsi miqdarında artacaqdır. Dünyada olan bank siteminin təməli bunun üzərində qurulubdur və bu məntiqdən irəli gələrək iqtisadçıların fikrincə vaxt- puldur.
İndi isə gəlin bu məsələyə əks tərəfədən baxaq. Misal üçün, tutaq ki, A müəssisi B müəssisəsinə iki ildən sonra 1 210 manat məbləğində borc ödəməlidir. Bunun yerinə A müəssisəsi, bu gün B müəssisəsinə 1 000 manat pul ödəyir, B müəssisəsi isə bu məbləği illik 10% dərəcə ilə bank depozit hesabına qoyur. Və iki ildən sonra bankdakı depozit hesabından 1 210 manat pul çıxardır. Gördüyümüz kimi, bu gün əlimizdə olan 1 000 manat iki ildən sonra bərabərdir 1 210 manata. Nəticə etibarı ilə B müəssisəsi üçün əslində heç bir fərq etmir, o bu gün 1 000 manat alacaq, yoxsa iki ildən sonra 1 210 manat.
A müəssisəsi iki ildən sonra B müəssisəsinə 1 210 manat məbləğində ödəniş etməlidir. Bu borc məbləğinin bu günə dəyəri nə qədər olacaqdır?
Bu borc məblğinin bu günə olan dəyərini hesablamaq üçün əksinə edərək, borc məbləğini 1 210 manatı, (1 + 0.10)2 əmsalına bölmək lazımdır:
1 210 / (1 + 0.10)2 = 1 000.
Bu əməliyyata diskontlaşdırma deyilir.
Beləliklə, diskontlaşdırma bir neçə ildən sonra ödəniləcək (və ya alınacaq) məbləğin bu günə dəyərinin hesablanmasına deyilir.
Gələcəkdə ödəyəcəyiniz və ya alacağınız məbləğin bu günə olan dəyərini bilmək istəyirsinizsə bu məbləği müəyyən faiz dərəcəsi ilə diskontlaşdırmaq lazımdır. Bu faiz dərəcəsinə "diskontlaşdırma dərəcəsi" deyilir. Hər iki misalda diskontlaşdırma dərəcəsi 10%-dir. 1 210 manat iki ildən sonra ödəniləcək məbləğdir, 1 000 manat isə gələcəkdə ödənilən məbləğin bugünə diskontlaşdırılmış dəyəridir. Məbləğlərin gələcəkdəki və bu günkü (diskontlaşdırılmış) dəyərlərinə inqilis dilində müvafiq olaraq future value (FV) və present valur (PV) deyilir. Misalda 1 210 manat - gələcəkdəki dəyərdir (FV), 1 000 manat isə bugünkü dəyərdir Diskontlaşdırma əməliyyatı etdikdə biz gələcəkdəki məbləğin bu gününkü dəyərini hesablayırıq:
Mürəkkəb faiz hesabladıqda isə əksinə biz bu günkü məbləğin gələcəkdə dəyərini hesablayırıq:
Diskontlaşdırılmış dəyəri hesablamaq üçün düstur və ya diskontlaşdırma düsturu ikinci misalda olacaqdır: 1 210 * 1/(1+R)n = 1 000.
Diskontlaşdırmanın riyazı düsturu belə olacaqdır:
PV = FV * 1/(1+R)n
Burada PV(present value) - bugünkü dəyər, FV(future value) - gələcəkdəki dəyər, R - faiz dərəcəsi, n - illər (gələcəkdəki tarixdən bu günə kimi).
Düsturun 1/(1+R) - hissəsinə diskontlaşdırma əmsalı da deyilir.
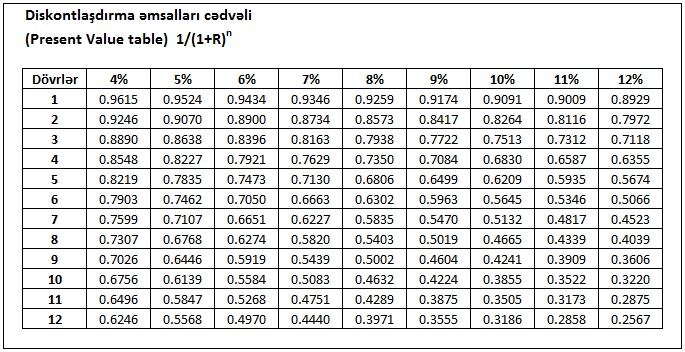
Diskontlaşdırma əmsalı, gördüyümüz kimi, faiz dərəcəsindən (R) və illərin sayından (n) asılıdır. Diskontlaşdırma əmsalını hər dəfə hesablamamaq üçün diskontlaşdırma əmsalı cədvəlindən rahat istifadə etmək olar. Bu cədvəldə faiz dərəcəsindən və illərdən asılı olaraq diskontlaşdırma əmsalları verilir. Bəzən bu cədvələ "diskontlaşdırma cədvəli" də deyirlər. Diskontlaşdırma cədvəlindəki əmsallar vergüldən sonra dördüncü rəqəmə kimi verilir.
Diskontlaşdırma əmsalları cədvəlini yükləmək. MS Excel
Bu cədvəldən istifadə hesablamanı asanlaşdırır: faiz dərəcəsi və illər verilibdirsə, misal üçün, faiz dərəcəsi 12%, il isə 5 ildirsə, o zaman, diskontlaşdırma əmsalı müvafiq sətir və sütunun kəsişməsində olacaqdır - 0.5674.
Müəssisə avadanlıq satır. Avadanlığın qiyməti 120 000 manatdır. Müştərinin təklifinə görə, o, avadanlığa görə ödənişi 3 ildən sonra, lakin 150 000 manat məbləğində edə bilər. Maliyyə şöbəsi satışın 2 variantını nəzərdən keçirir. Birinci halda, avadanlıq 120 000 manata nağd satılır, ikinci halda isə satılmış avadanlığa görə ödəniş 3 ildən sonra ediləcəkdir. Lakin, bu zaman, avadanlığın qiyməti 150 000 manat olacaqdır. Hansı variant müəssisə üçün daha sərfəlidir? Gəlin bunu hesablayaq.
Nəzərə alsaq ki, 3 illik depozit üzrə banklarda faiz dərəcəsi təxminən 10%-dir, o zaman, biz 3 ildən sonra alacağımız 150 000 manatın bugünkü dəyərini hesablaya bilərik.
Diskontlaşdırma cədvəlində 10% və 3 il üçün müvafiq əmsal olacaqdır - 0.7513. Bu o deməkdir ki, bu gün aldığımız 0.75 manat, 10% dərəcə ilə 3 ildən sonra 1 manat olacaqdır.
Beləliklə, 150 000 manat * 0.7513 = 112 695
112 695 manat - 3 ildən sonra alacağımız 150 000 manatın bugünkü dəyəridir.
Hesablanan bu məbləğ nağd satış zamanı alınan 120 000 manatdan azdır. Çünki müəssisə bu gün 120 000 manat alarsa və bu məbləği bankda depozit hesabına qoyarsa, o zaman, 3 ildən sonra bu məbləğ olacaqdır: 120 000 * (1.1)3 = 159 720 manat.
Beləliklə, müəssisə üçün birinci variant, və ya 120 000 manatın bu gün ödənilməsi daha sərfəlidir.
Diskontlaşdırma sözünün kökü "diskont" sözüdür, və ingilis dilindən "endirim" kimi tərcümə edilir. Həqiqətəndə biz bu sözün yaranma zamanına geri gayıtsaq görərik ki, artıq 17-ci əsrdə bu söz "deduction for early payment" ("erkən ödənişə görə endirim") mənasında istifadə edilirdi. Hələ o zamanlar iş adamları hesablaşmalar apararkan "pulun zaman dəyərini" nəzərə alırdılar. Buradan diskontlaşdırma terminin daha bir izahını vermək olar - ödənişin daha erkən edilməsinə görə edilən endirimin hesablanması. Bu endirim elə "pulun zaman dəyərinin" ölçüsüdür və ya "time value of money".

Diskontlaşdırma
2019-08-22 | Maliyyə menecmenti |Maliyyə sahəsində bir çox hallarda (investisiyaların qoyulması, səhmlərin alınması, yeni layihələrin qiymətləndirilməsi və s. hallarda) məbləğlərin diskontlaşdırılmasından istifadə edilir. Bundan başqa, məbləğlərin diskontlaşdırılmasını bir çox maliyyə hesabatlarının beynəlxalq standartları tələb edir:
- Müştərilərlə müqavilələr üzrə gəlirlər. IFRS 15;
- "İcarələr. İFRS 16";
- Aktivlərin Qiymətdən düşməsi. IAS 36;
- Yaradılmış ehtiyat fondları, Şərti öhdəliklər və Şərti aktivlər. IAS 37;
- Maliyyə alətləri: Tanınma və ölçülmə. IAS 39 və s.
Misal üçün, "İcarələr. İFRS 16" standartında icarə müddətinin başlanması tarixində icarəçi icarə öhdəliyini həmin tarixdə ödənilməmiş icarə ödənişlərinin diskontlaşdırılmış dəyərilə ölçməlidir.
Bəs məbləğin diskontlaşdırılması nədir? Nə cür hesablanır?
Diskontlaşdırmanın mahiyyətini izah etmək üçün gəlin bu əməliyyatın izahını sondan başlayaq.
Müəssisə bankda depozit hesab açmışdır və hesaba 2 illik müddətinə 1 000 manat əmanət qoymuşdur. Əmanət üzrə illik faiz dərəcəsi 10%-dir. Bir ildən sonra bu məbləğ 1 100 manat olacaqdır: əsas məbləğ 1 000 manat + faiz əlavəsi 100 manat (1 000*10%). Bir ildən sonra siz hesabdan 1 100 manat çıxara bilərsiniz.
Riyazi olaraq düstur bu cür olacaqdır
1 000 * (1+10%) və ya 1 000 * (1.10) = 1 100
İki ildən sonra 1 000 manat olacaqdır 1 210 manat (1 000 manat + birinci ilin faizi 100 manat + ikinci ilin faizi 110 = 1 100*10%). İki il üzrə bankda olan əmanət hesabının artım düsturu olacaqdır: (1 000*1.10)*1.10 = 1 210.
İllər keçdikcə əmanətin məbləği artacaqdır. Bankdan alacağınız məbləğin faizini bir, iki, üç və s. ilərdən sonra müəyyən etmək üçün əmanət məbləğini əmsala vurmaq lazımdır:
(1+R)n
Burada:
- R - faiz dərəcəsi (10% və ya 0.10);
- n - illər.
Bizim misalda olacaqdır: 1 000 * (1 + 0.10)2 = 1 210.
Misaldan göründüyü kimi iki ildən sonra bank depozitində olan pulun məbləği illik bank faizinin dərəcəsindən asılıdır. Əmanətlər üzrə illik bank faizi çox olduqca məbləğ də artacaqdır. Əmanətlər üzrə bankın illik faiz dərəcəsi 12% olsa idi, iki ildən sonra müəssisə bankdan 1 254.40 manat götürə biləcəkdi: 1 000 * (1+0.12)2 = 1 254.40.
Beləliklə, bu üsul ilə depozitə qoyulan məbləğin istənilən ildən sonra məbləğini hesablamaq mümkündür. Pulun gələcəkdə dəyərinin hesablanmasına inqilis dilində "compoundinq" deyilir. Azərbaycan dilində bu termin "mürəkkəb faizin hesablanması" kimi tərcümə edilir. Bu termini "faizlərin toplanması" kimi də tərcümə etmək olar.
Aydındır ki, banka qoyulmuş əmanətlər illər keçdikcə illik faiz dərəcəsi miqdarında artacaqdır. Dünyada olan bank siteminin təməli bunun üzərində qurulubdur və bu məntiqdən irəli gələrək iqtisadçıların fikrincə vaxt- puldur.
İndi isə gəlin bu məsələyə əks tərəfədən baxaq. Misal üçün, tutaq ki, A müəssisi B müəssisəsinə iki ildən sonra 1 210 manat məbləğində borc ödəməlidir. Bunun yerinə A müəssisəsi, bu gün B müəssisəsinə 1 000 manat pul ödəyir, B müəssisəsi isə bu məbləği illik 10% dərəcə ilə bank depozit hesabına qoyur. Və iki ildən sonra bankdakı depozit hesabından 1 210 manat pul çıxardır. Gördüyümüz kimi, bu gün əlimizdə olan 1 000 manat iki ildən sonra bərabərdir 1 210 manata. Nəticə etibarı ilə B müəssisəsi üçün əslində heç bir fərq etmir, o bu gün 1 000 manat alacaq, yoxsa iki ildən sonra 1 210 manat.
A müəssisəsi iki ildən sonra B müəssisəsinə 1 210 manat məbləğində ödəniş etməlidir. Bu borc məbləğinin bu günə dəyəri nə qədər olacaqdır?
Bu borc məblğinin bu günə olan dəyərini hesablamaq üçün əksinə edərək, borc məbləğini 1 210 manatı, (1 + 0.10)2 əmsalına bölmək lazımdır:
1 210 / (1 + 0.10)2 = 1 000.
Bu əməliyyata diskontlaşdırma deyilir.
Beləliklə, diskontlaşdırma bir neçə ildən sonra ödəniləcək (və ya alınacaq) məbləğin bu günə dəyərinin hesablanmasına deyilir.
Gələcəkdə ödəyəcəyiniz və ya alacağınız məbləğin bu günə olan dəyərini bilmək istəyirsinizsə bu məbləği müəyyən faiz dərəcəsi ilə diskontlaşdırmaq lazımdır. Bu faiz dərəcəsinə "diskontlaşdırma dərəcəsi" deyilir. Hər iki misalda diskontlaşdırma dərəcəsi 10%-dir. 1 210 manat iki ildən sonra ödəniləcək məbləğdir, 1 000 manat isə gələcəkdə ödənilən məbləğin bugünə diskontlaşdırılmış dəyəridir. Məbləğlərin gələcəkdəki və bu günkü (diskontlaşdırılmış) dəyərlərinə inqilis dilində müvafiq olaraq future value (FV) və present valur (PV) deyilir. Misalda 1 210 manat - gələcəkdəki dəyərdir (FV), 1 000 manat isə bugünkü dəyərdir Diskontlaşdırma əməliyyatı etdikdə biz gələcəkdəki məbləğin bu gününkü dəyərini hesablayırıq:
Mürəkkəb faiz hesabladıqda isə əksinə biz bu günkü məbləğin gələcəkdə dəyərini hesablayırıq:
Diskontlaşdırılmış dəyəri hesablamaq üçün düstur və ya diskontlaşdırma düsturu ikinci misalda olacaqdır: 1 210 * 1/(1+R)n = 1 000.
Diskontlaşdırmanın riyazı düsturu belə olacaqdır:
PV = FV * 1/(1+R)n
Burada PV(present value) - bugünkü dəyər, FV(future value) - gələcəkdəki dəyər, R - faiz dərəcəsi, n - illər (gələcəkdəki tarixdən bu günə kimi).
Düsturun 1/(1+R) - hissəsinə diskontlaşdırma əmsalı da deyilir.
Diskontlaşdırma əmsalı, gördüyümüz kimi, faiz dərəcəsindən (R) və illərin sayından (n) asılıdır. Diskontlaşdırma əmsalını hər dəfə hesablamamaq üçün diskontlaşdırma əmsalı cədvəlindən rahat istifadə etmək olar. Bu cədvəldə faiz dərəcəsindən və illərdən asılı olaraq diskontlaşdırma əmsalları verilir. Bəzən bu cədvələ "diskontlaşdırma cədvəli" də deyirlər. Diskontlaşdırma cədvəlindəki əmsallar vergüldən sonra dördüncü rəqəmə kimi verilir.
Diskontlaşdırma əmsalları cədvəlini yükləmək. MS Excel
Bu cədvəldən istifadə hesablamanı asanlaşdırır: faiz dərəcəsi və illər verilibdirsə, misal üçün, faiz dərəcəsi 12%, il isə 5 ildirsə, o zaman, diskontlaşdırma əmsalı müvafiq sətir və sütunun kəsişməsində olacaqdır - 0.5674.
Müəssisə avadanlıq satır. Avadanlığın qiyməti 120 000 manatdır. Müştərinin təklifinə görə, o, avadanlığa görə ödənişi 3 ildən sonra, lakin 150 000 manat məbləğində edə bilər. Maliyyə şöbəsi satışın 2 variantını nəzərdən keçirir. Birinci halda, avadanlıq 120 000 manata nağd satılır, ikinci halda isə satılmış avadanlığa görə ödəniş 3 ildən sonra ediləcəkdir. Lakin, bu zaman, avadanlığın qiyməti 150 000 manat olacaqdır. Hansı variant müəssisə üçün daha sərfəlidir? Gəlin bunu hesablayaq.
Nəzərə alsaq ki, 3 illik depozit üzrə banklarda faiz dərəcəsi təxminən 10%-dir, o zaman, biz 3 ildən sonra alacağımız 150 000 manatın bugünkü dəyərini hesablaya bilərik.
Diskontlaşdırma cədvəlində 10% və 3 il üçün müvafiq əmsal olacaqdır - 0.7513. Bu o deməkdir ki, bu gün aldığımız 0.75 manat, 10% dərəcə ilə 3 ildən sonra 1 manat olacaqdır.
Beləliklə, 150 000 manat * 0.7513 = 112 695
112 695 manat - 3 ildən sonra alacağımız 150 000 manatın bugünkü dəyəridir.
Hesablanan bu məbləğ nağd satış zamanı alınan 120 000 manatdan azdır. Çünki müəssisə bu gün 120 000 manat alarsa və bu məbləği bankda depozit hesabına qoyarsa, o zaman, 3 ildən sonra bu məbləğ olacaqdır: 120 000 * (1.1)3 = 159 720 manat.
Beləliklə, müəssisə üçün birinci variant, və ya 120 000 manatın bu gün ödənilməsi daha sərfəlidir.
Diskontlaşdırma sözünün kökü "diskont" sözüdür, və ingilis dilindən "endirim" kimi tərcümə edilir. Həqiqətəndə biz bu sözün yaranma zamanına geri gayıtsaq görərik ki, artıq 17-ci əsrdə bu söz "deduction for early payment" ("erkən ödənişə görə endirim") mənasında istifadə edilirdi. Hələ o zamanlar iş adamları hesablaşmalar apararkan "pulun zaman dəyərini" nəzərə alırdılar. Buradan diskontlaşdırma terminin daha bir izahını vermək olar - ödənişin daha erkən edilməsinə görə edilən endirimin hesablanması. Bu endirim elə "pulun zaman dəyərinin" ölçüsüdür və ya "time value of money".


